Pozwala w szybki i czytelny sposób dokonać wizualizacji związku zaobserwowanego w tabeli kontyngencji. Szczegółowy artykuł poświęcony procedurze przekształcania danych z tabeli w mapę percepcyjną dociekliwy czytelnik odnajdzie w stosownym artykule. Dzięki opisanemu w tekście algorytmowi SVD, wartości odpowiadające poszczególnych profilom wierszowym i kolumnowym zamieniane są przez silnik analityczny SPSS/PS IMAGO PRO na współrzędne w typowym układzie odniesienia.
Odpowiedź na pytanie, jak przedstawić podobieństwo pomiędzy kategoriami dwóch zmiennych jakościowych w języku geometrii, ma kluczowe znaczenie dla zrozumienia istoty działania algorytmu analizy korespondencji oraz właściwego wyboru normalizacji, a co za tym idzie – dla prawidłowej interpretacji mapy percepcyjnej będącej wynikiem analizy.
Zacznijmy od krótkiego przypomnienia, w jaki sposób obliczyć dystans pomiędzy dwoma obiektami. Podejść jest zaskakująco wiele, jednak na potrzeby niniejszego tekstu skupmy się na najbardziej intuicyjnym sposobie pomiaru, czyli znanym z lekcji geometrii dystansie euklidesowym. Wyraża on najmniejszą możliwą odległość pomiędzy dwoma punktami umieszczonymi na płaszczyźnie, lub w dowolnej, wielowymiarowej przestrzeni.
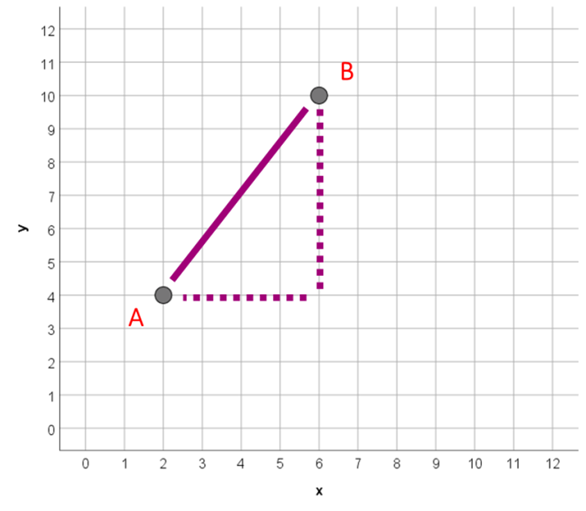
Obliczanie odległości na płaszczyźnie
Odległość euklidesowa to pierwiastek z sumy kwadratów odległości na poszczególnych wymiarach. Część czytelników słusznie dostrzeże tutaj analogię do obliczania długości przeciwprostokątnej trójkąta prostokątnego. Warto jednak zaznaczyć, że odległość może być obliczona również w przestrzeni posiadającej 3 a nawet więcej wymiarów.
Ile więc wynosi odległość między punktami przedstawionymi na powyższym wykresie? (6-2)2 + (10-4)2=16+36=52. Dystans pomiędzy analizowanymi punktami to pierwiastek z 52 czyli około 7,21.
A jak powyższe obliczenia mają się do odległości pomiędzy kategoriami zmiennych umieszczonych w tabeli? Rozważmy przykład. Konsumentów zapytano o to, czym przede wszystkim kierują się przy wyborze piwa, zadając im dodatkowo pytanie o poziom wykształcenia. Zamieszczona poniżej tabela zawiera zestawione odpowiedzi koneserów tego szlachetnego trunku. Dla ułatwienia odczytu została ona pokolorowana gradientem za pomocą procedury kolorowania tabeli dostępnej w PS IMAGO PRO.

Główne kryterium wyboru piwa w zależności od poziomu wykształcenia
Tabela zawiera profile kolumnowe (procentowanie w kolumnach), czyli informację jaki odsetek osób w danej kategorii wykształcenia kierował się danym motywem przy wyborze piwa (wskazywano najważniejszy powód). Widzimy, że wykształcenie wyraźnie różnicowało motywacje. Cena i zawartość alkoholu były najważniejszymi motywami dla osób z wykształceniem podstawowym i zawodowym, osoby z wykształceniem średnim kierowały się głównie estetycznym opakowaniem, natomiast piwosze z wykształceniem wyższym najczęściej uzasadniali swój wybór znaną marką oraz ceną.
Kategorie zmiennej kolumnowej różnią się od siebie, widzimy jednak wyraźnie (co podkreśla zastosowanie kolorowania tabeli), że osoby z wykształceniem podstawowym i zasadniczym kierują się zbliżonymi pobudkami, natomiast osoby z wykształceniem średnim i wyższym cechują się odmiennym wzorcem motywacji przy wyborze piwa. Osoby z wykształceniem podstawowym będą więc bliższe osobom z wykształceniem zasadniczym niż respondentom z wykształceniem wyższym.
Jak to jednak obliczyć? Wyobraźmy sobie (choć może to stanowić pewne wyzwanie), że każda kolumna to punkt leżący w sześciowymiarowej przestrzeni. Poszczególne kategorie wierszowe (cena, smak itd.) stanowią w tej przestrzeni osie układu współrzędnych, a poszczególne wartości, które możemy odczytać z kolumny odpowiadającej osobom z wykształceniem podstawowym to nic innego jak współrzędne w tym układzie. Punkt „podstawowe” miałby więc następujące współrzędne [0,402; 0,287; 0,080; 0,046; 0,080; 0,103]. W analogiczny sposób odczytujemy współrzędne każdego punktu odpowiadającego kategorii zmiennej kolumnowej.
Przy obliczaniu dystansu musimy uwzględnić jeszcze jedną ważną informację. Przyjrzyjmy się przeciętnemu profilowi kolumnowemu (ostatnia kolumna „ogółem”), która zawiera udział poszczególnych kategorii zmiennej wierszowej w badanej próbie. Widzimy, że znajdujące się tam proporcje brzegowe znacząco się różnią: łącznie ceną kierowało się aż 29,4% badanych, natomiast składnikami tylko 7,9%. Jest to analogiczna sytuacja do tej, gdybyśmy prezentując związek posługiwali się zmiennymi o różnych miarach (np. wzrost w cm i waga w kg) do obliczenia dystansu. Zmienna o większym zakresie wartości zdominowałaby nasze rozwiązanie. Dlatego przed obliczeniem dystansu musimy posłużyć się doskonale znaną analitykom procedurą standaryzacji.
Jak wystandaryzować nasze wymiary? Wystarczy obliczony kwadrat odległości na każdym z wierszowych wymiarów podzielić przez odpowiadającą poszczególnym wierszom proporcję brzegową z ostatniej kolumny. Taki „standaryzowany” dystans nazywany jest „ważonym dystansem euklidesowym” lub dystansem Chi-kwadrat.Ile wynosi więc ważona odległość euklidesowa pomiędzy wykształceniem podstawowym a zawodowym? Obliczmy to:
(0,402 - 0,337)2/0,294 + (0,287 - 0,337)2/0,178 + (0,080 - 0,120)2/0,105 + (0,046 - 0,048)2/0,192 + (0,080 - 0,060)2 /0,079 + (0,103 - 0,096)2/0,153 = 0,049
Pierwiastek z tej wartości to 0,222 i jakkolwiek abstrakcyjnie by to nie brzmiało, tyle wynosi nasza poszukiwana odległość. Dla porównania, odległość pomiędzy punktem reprezentującym wykształcenie podstawowe a wyższe wynosi 0,889, a więc leży on zdecydowanie dalej w naszej sześciowymiarowej przestrzeni. Obliczenia pozostawiam czytelnikom do przeprowadzenia w ramach ćwiczeń. Jak obliczyć odległości pomiędzy punktami na mapie percepcyjnej? Poniżej zaprezentowany został fragment tabeli będący wynikiem analizy korespondencji przeprowadzonej na danych przedstawionych w Tabeli 1. Zawiera on współrzędne („wartość na wymiarze”), które zostały podczas analizy przypisane poszczególnym kategoriom wykształcenia.
Analiza została przeprowadzona w normalizacji kolumnowej, punkty mają nadane współrzędne główne. Oznacza to, że odległości pomiędzy nimi mogą być porównywane, ponieważ dystans euklidesowy pomiędzy dwoma kategoriami tej samej zmiennej posiada interpretację w kategoriach odległości Chi-kwadrat. Należy podkreślić, że zaprezentowane poniżej rozwiązanie jest trzywymiarowe, co stanowi pełne odwzorowanie zróżnicowania pierwotnej tabeli kontyngencji, a zatem i pełną porównywalność odległości pomiędzy punktami. Analiza korespondencji zamieniła sześciowymiarową tabelę w trzywymiarową mapę percepcyjną.
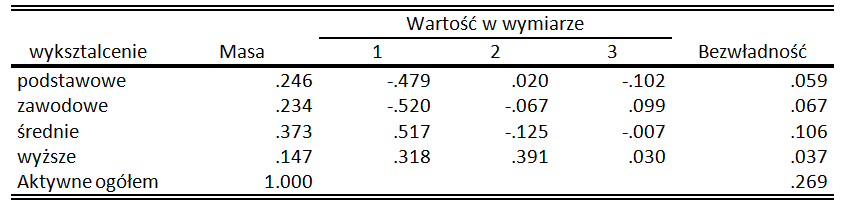
Współrzędne punktów kolumnowych – analiza korespondencji
Aby obliczyć odległość pomiędzy punktem odpowiadającym wykształceniu podstawowemu a zawodowemu w przestrzeni, należy zsumować kwadraty odległości na poszczególnych wymiarach a następnie z obliczonej wartości wyciągnąć pierwiastek. Obliczenia będą wyglądały następująco: (-0,479 + 0,520)2 + (0,020 + 0,067)2 + (-0,102 - 0,099)2 = 0,049. Pierwiastek z tej wartości wynosi 0,222 i to jest właśnie nasza odległość – dokładnie tyle samo ile wynosi odległość obliczona na podstawie wartości profili kolumnowych z tabeli kontyngencji. A jak ma się do tego dystans pomiędzy wykształceniem podstawowym a wyższym? (-0,479 - 0,318)2 + (0,020 - 0,391)2 + (-0,102 - 0,030)2 = 0,790, co po spierwiastkowaniu daje odległość 0,889. Punkt opisujący wykształcenie wyższe znajduje się na mapie zdecydowanie dalej od kategorii „podstawowe” niż punkt przypisany do wykształcenia zasadniczego.

Współrzędne punktów kolumnowych – mapa percepcyjna
Na zakończenie rozwiążmy jeszcze jedną zagadkę – dlaczego ważony dystans euklidesowy nazywany jest metryką Chi-kwadrat. Przypomnijmy, że wartość Chi-kwadrat dla danej tabeli, to suma kwadratów reszt standaryzowanych. Reszta standaryzowana to różnica między wartością obserwowaną a oczekiwaną, podzielona przez pierwiastek z liczebności oczekiwanej. Wróćmy na moment do tabeli przedstawionej na początku tekstu. Dla ułatwienia spróbujmy obliczyć odległość pomiędzy dowolną kategorią wykształcenia a profilem przeciętnym (kolumną ogółem) na pierwszym wymiarze. Na wymiarze „cena”, odległość między wykształceniem podstawowym a profilem przeciętnym równa się pierwiastkowi z wyrażenia (0,402 - 0,294)2/0,294. Przyjrzymy się tym wartościom. Ile wynosiłyby procenty w każdym profilu kolumnowym, gdyby między wykształceniem a motywem wyboru piwa nie byłoby związku – dokładnie tyle, ile wynoszą wartości znajdujące się w profilu przeciętnym. We wzorze na odległość pojawia się różnica pomiędzy rzeczywistym procentem kolumnowym (czyli wartością empiryczną) a procentem z profilu przeciętnego (wartością oczekiwaną przy braku związku). Teraz różnicę wystarczy jeszcze podzielić przez pierwiastek procentu z profilu przeciętnego w celu standaryzacji wymiarów (znów wartość oczekiwana), by analogia do metody obliczania reszty standaryzowanej i wartości statystyki Chi-kwadrat stała się oczywista. Zagadka rozwiązana!
W powyższym tekście została zaprezentowana metoda obliczania dystansów pomiędzy kategoriami zmiennej przedstawionej w tabeli kontyngencji oraz na mapie percepcyjnej. Podobieństwo profili obserwowane w tabeli, jest po kilku przekształceniach przekładalne na wyniki przedstawione na mapie percepcyjnej, będącej efektem analizy korespondencji. Technika ta kryje w sobie jeszcze wiele równie interesujących powiązań z geometrią i fizyką, co powinno stanowić dodatkową zachętę do zgłębiania jej wszystkich tajników i praktycznego wykorzystania w analizie danych.